Teorema chino

Teorema chino

Sean m1, m2, …, mn enteros positivos primos relativos entre si. El sistema

x ≡ a1 (mod m1)
x ≡ a2 (mod m2)
…
x ≡ an (mod mn)

tiene una solución única módulo m= m1m2…mn,

x ≡ a1M1y1 + a2M2y2 + … + anMnyn

donde Mk = m/mk y además Mkyk º 1 (mod mk)

Encuentre m = m1* m2 * …* mn

Encuentre Mk=m/mk, para k=1,2,…,n
Encuentre n inversos, uno para cada Mk mod mk
Establezca la solución como

X = a1M1y1 + a2M2y2 + . . . + anMnyn

Aplicaciones del Teorema Chino

El teorema chino del resto tiene importantes aplicaciones en criptografía, en especial para reducir operaciones con números enormes mediante el paso a congruencias. En el algoritmo RSA, por ejemplo, los cálculos se hacen módulo n, donde n es un producto de dos primos p y q. Tamaños habituales para n son 1024, 2048 ó 4096 bits, haciendo que los cálculos requieran una gran cantidad de tiempo. Usando el teorema chino del resto los cálculos pueden ser transportados del anillo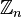 al anillo . La suma de las longitudes de bit de p y q es la longitud de bit de n, haciendo p y q considerablemente menor que n. Esto acelera mucho los cálculos. Nótese que las implementaciones del algoritmo RSA usando el teorema chino del resto son más susceptibles a ataques de "fault injection".